Exposant fractionnaire
Regardez d'autres dictionnaires:
fractionnaire — [ fraksjɔnɛr ] adj. • 1725; de fraction 1 ♦ Math. Qui est écrit sous forme de fraction. Nombre fractionnaire. Expression algébrique fractionnaire. Exposant fractionnaire. Partie fractionnaire d un réel : différence entre ce réel et sa partie… … Encyclopédie Universelle
Mouvement brownien fractionnaire — Le mouvement Brownien fractionnaire (mBf) a été introduit par Kolmogorov en 1940 comme moyen d engendrer des spirales gaussiennes dans des espaces de Hilbert. Mandelbrot et Van Ness (1968) l ont rendu célèbre en l introduisant dans des modèles… … Wikipédia en Français
Idéal fractionnaire — Richard Dedekind donne en 1876 la définition d idéal fractionnaire. En mathématiques, et plus précisément en théorie des anneaux, un idéal fractionnaire est une généralisation de la définition d un idéal. Ce concept doit son origine à la théorie… … Wikipédia en Français
Racine (Mathématiques) — Racine d un nombre En mathématiques, une racine n ième d un nombre a est un nombre b tel que bn = a, où n est un entier naturel non nul, Selon que l on travaille dans l ensemble des réels positifs, l ensemble des réels ou l ensemble des complexes … Wikipédia en Français
Racine N-ième — Racine d un nombre En mathématiques, une racine n ième d un nombre a est un nombre b tel que bn = a, où n est un entier naturel non nul, Selon que l on travaille dans l ensemble des réels positifs, l ensemble des réels ou l ensemble des complexes … Wikipédia en Français
Racine d'un nombre — En mathématiques, une racine n ième d un nombre a est un nombre b tel que bn = a, où n est un entier naturel non nul, Selon que l on travaille dans l ensemble des réels positifs, l ensemble des réels ou l ensemble des complexes, le nombre de… … Wikipédia en Français
Racine n-ieme — Racine d un nombre En mathématiques, une racine n ième d un nombre a est un nombre b tel que bn = a, où n est un entier naturel non nul, Selon que l on travaille dans l ensemble des réels positifs, l ensemble des réels ou l ensemble des complexes … Wikipédia en Français
Racine n-ième — Racine d un nombre En mathématiques, une racine n ième d un nombre a est un nombre b tel que bn = a, où n est un entier naturel non nul, Selon que l on travaille dans l ensemble des réels positifs, l ensemble des réels ou l ensemble des complexes … Wikipédia en Français
Racine nième — Racine d un nombre En mathématiques, une racine n ième d un nombre a est un nombre b tel que bn = a, où n est un entier naturel non nul, Selon que l on travaille dans l ensemble des réels positifs, l ensemble des réels ou l ensemble des complexes … Wikipédia en Français
Racine Énième — Racine d un nombre En mathématiques, une racine n ième d un nombre a est un nombre b tel que bn = a, où n est un entier naturel non nul, Selon que l on travaille dans l ensemble des réels positifs, l ensemble des réels ou l ensemble des complexes … Wikipédia en Français

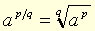 (
(